WAEC Mathematics Past Questions

WAEC Mathematics Past Questions

Below are Mathematics Past Questions Read Carefully 

Question 1

A = {2, 4, 6, 8}, B = {2, 3, 7, 9} and C = {x: 3 < x < 9} are subsets of the universal-set 

U = {2, 3, 4, 5, 6, 7, 8, 9}. Find 

(a)   A n(B'nC');

(b) (AuB) n(BuC).

Observation

However question was reportedly attempted by majority of the candidates and their performance was described as satisfactory. Many of them lost some marks because they failed to use curly brackets to enclose the elements of the sets. A good number of the candidates were also reported not to have listed the elements of set C hence, were not able to find its complement while others did not separate the elements of a set with comas.

Candidates were expected to list the elements of C i.e. C = {4, 5,6, 7, 8}, obtain the compliments of the sets Band C thus B' = {4,5,6, 8}, C' = {2, 3, 9,}. Using these sets, the following procedures were to be followed: 

(a)(B' nC') = { } Hence An (B' n C') = { }. Some candidates were reported to have written { 0 } instead of { } or 0. 

(b) (A u B) = { 2, 3,4,6, 7, 8, 9 }, (BuC) = {2, 3, 4,5,6, 7, 8, 9 } Therefore { Au B } n (BuC) = { 2, 3, 4, 6, 7, 8, 9 }.

Question 2

(a) The angle of depression of a boat from the mid-point of a vertical cliff is 35°. If the boat is 120 m from the foot of the cliff, calculate the height of the cliff.

(b) Towns P and Q are x km apart. Two motorists set out at the same time from P to Q at steady speeds of 60 km/h and 80 km/h. The faster motorist got to Q 30 minutes earlier than the other. Find the value of x.

Observation

This question was also reported to have been attempted by majority of the candidates. Furthermore, the report stated that in part (a), majority of the candidates could not draw the diagram correctly and this affected their performance significantly. A few others were unable to apply the trigonometric ratios correctly. Candidates were expected to draw the diagram.

From the diagram, I FMI :: 120 tan 35° = 84.02m. Therefore the height of the cliff:: 2 x 84.02 = 168.04. 

In part (b), the most observed weakness was their inability to convert from minutes to hours. They were expected to recall that time :: distance (i.e. t:: ~) and apply this to the problem. 

                                                         speed         v 

Time taken by faster motorist « ~ while that of the other motorist = ~ where x is the distance 

                                                             60                                                                   80 

                     X x 

from P to Q. - - - = Y2 (30 rnlnutes « Y2 hr). Simplifying this expression gave x = 120km. 

                       60 80 

Candidates' responses to this question were reported to be generally below average.

Question 3

(a) In the diagram, L PQR = 125°, LQRS = r, LRST = 800 and LSTU = 44°. Calculate the value of r

b) .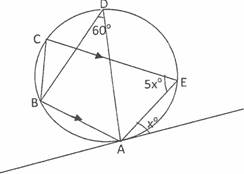

In the diagram, TS is a tangent to the circle at A. ABI ICE, LAEC = sx", LADB = 60° and LTAE = xo. Find the value of x",

Observation

Part (a) of this question required that candidates drew straight lines, one each passing through points Sand R and parallel to PQ and UT as shown in the diagram below but the report stated that majority of the candidates did not.From the diagram, LMQR = LQRN = 180 -125 = 55° ( alternate angles), LVST = 44° (alternate angle to LSTU). Therefore LNRS = LVSR = 80 - 44° = 360• Hence, r = 55 + 36 = 91°

In part (b), candidates' performance was reported to be worse than part (a). Candidates were reported to have exhibited poor understanding of circle theorems. Teachers were encouraged to do a lot of work in this area.

From the diagram, LBDA = LBAS = 600 (angles in the alternate segment). LBAE = 180° - 5x (adjacent angles on a transversal). Therefore LBAS + LBAE + LEAT = 60 + 180 - 5x + x = 180 (angles on a straight line). Solving this simple equation gave x = 150. Candidates' performance this question was described as poor.

Question 4

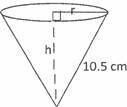
The diagram shows a cone with slant height 10.5 cm. If the curved surface area of the cone is 115.5 cm²;, calculate, correct to 3 significant figures, the: 

(a)base radius, r; 

 (b)height, h; 

(c)volume of the cone. [Taken= 22]

                                                          7 

Observation

This question was reported as one of the questions where candidates performed very well. They showed good understanding of mensuration of right circular cones as they were able to apply relevant formulae and majority of them obtained full marks. The curved surface area, 

iu! = 115.5cm², slant height,l= 10.scm, n = ll, hence r = 115.5

                                                                                                     7nl 

= 11.5 x 7 = 3.S0cm. r2 + h2 = (10.5}2 => h = .J(10.5)2 - (3.5)2 = 9.90cm 

   22 x 10.5 

Volume of cone = .1 x 22 x 3.5 x 9.899 == 127 cm² 

                                                     3 7                 1 

A good number of the candidates were however reported to have lost some marks, especially the A marks, because they did not give their answers in 3 significant figures as required by the question.

Question 5

Two fair dice are thrown. 

M is the event described by "the sum of the scores is 10" and 

N is the event described by "the difference between the scores is 3". 

(a) Write out the elements of M and N. 

(b) Find the probability of M or N. 

(c) Are M and N mutually exclusive? Give reasons.

Observation

This question was reported to be popular and well attempted by majority of the candidates. However, a few of them did not list the elements of M and N as required but drew the sample space when 2 dice are thrown. Some of them who listed these elements did not do so completely. Majority of them were reported not to be able to state correctly the condition for which events are mutually exclusive. Candidates were expected to show that M = { (4,6) , (5,5), (6,4}. N = { (1,4), (2,5), (3,6), (4,1), 

(5,2), (6,3) }. Probability of M = 3/36 = 1/12. Probability of N = 6/36 = 1/6. 

Question 6

(a) The scale of a map is 1:20,000. Calculate the area, in square centimetres, on the map of a forest reserve which covers 85 km², 

(b) A rectangular playing field is 18 m wide. It is surrounded by a path 6m wide such that its area is equal to the area of the path. Calculate the length of the field.

(c]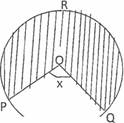 

Observation

Candidates' performance in part (a) was reported to be poor. A good number of them were reported not to have attempted this part of the question. They were expected to recall that lkm = 100,000 ern, therefore 1km2 = 1km x 1km = 100,000 x 100,000 = 10,000 000,OOOcm2• 

85km2 = 850,000,000,000 cm². 20,000 em on the ground = 1 cm on the map, hence 400,000,000 cm² on the ground = 1 cm2850,000,000,000 = 2125 cm2 on the map.                                                                                                                                        400,000,000 

In part (b), candidates' performance was said to be better than it was in part (a). However, many candidates did not draw the diagram correctly and so were not able to solve the problem. 

From the diagram, area of path = 2(30 x 6) + 12a = 360 + 12a. Area of field = 18a. Since they are equal, 18a = 12a + 360. This gave a = 60 m. 

In part (c), candidates' performance was described as fair. However, some candidates did not see the reflex angle as 360 - x, hence, did not subtract their final answer from 360° when they had calculated the value of the reflex angle. Here, 360 - x x 22x Z x Z = 27.5 cm2 

                                      360         7       2 2

This meant that 360 - x = 360 x 2 x 27.5 from where we obtain x = 103° to the nearest degree 

Question 7

(a) The scale of a map is 1:20,000. Calculate the area, in square centimetres, on the map of a forest reserve which covers 85 km", 

(b) A rectangular playing field is 18 m wide. It is surrounded by a path 6m wide such that its area is equal to the area of the path. Calculate the length of the field.

(c] 

Observation

Candidates' performance in part (a) was reported to be poor. A good number of them were reported not to have attempted this part of the question. They were expected to recall that lkm = 100,000 ern, therefore 1km2 = 1km x 1km = 100,000 x 100,000 = 10,000 000,OOOcm2• 

85km2 = 850,000,000,000 em". 20,000 em on the ground = 1 cm on the map, hence 400,000,000 em2 on the ground = 1 cm22 on the ground is equivalent to 850,000,000,000 = 2125 cm2 on the map.                                                                                                                                        400,000,000 

In part (b), candidates' performance was said to be better than it was in part (a). However, many candidates did not draw the diagram correctly and so were not able to solve the problem.

From the diagram, area of path = 2(30 x 6) + 12a = 360 + 12a. Area of field = 18a. Since they are equal, 18a = 12a + 360. This gave a = 60 m.

In part (c), candidates' performance was described as fair. However, some candidates did not see the reflex angle as 360 - x, hence, did not subtract their final answer from 360° when they had calculated the value of the reflex angle. Here, 360 - x x 22x Z x Z = 27.5 cm2 

                                      360        7       2 2

This meant that 360 - x = 360 x 2 x 27.5 from where we obtain x = 103° to the nearest degree

Question 8

Using ruler and a pair of compasses only,

(a) construct

(i) a quadrilateral PQRS with IPSI :: 6 cm, LRSP:: 90°,

IRSI = 9 ern, IQRI = 8.4 cm and IPQI :: 5.4 cm;

(ii) the bisectors of LRSP and LSPQ to meet at X;

(iii) The perpendicular XTto meet PS at T.

(b) Measure IXT/'

Observation

This question on geometrical construction was reported to be quite unpopular among the candidates. Very few of them attempted it and their performance was said to be poor. A good number of them measured the angles instead of constructing them. Others could not construct a perpendicular from a given point to a given line segment. Teachers are encouraged to emphasize this area of the syllabus

Question 9

In the diagram, /AB/ = 8 km, /BC/ = 13 km, the bearing of A from B is 310° and the bearing of B from C is 230°. Calculate, correct to 3 significant figures,

(a) the distance AC;

(b) the bearing of C from A;

(c) how far east of B, C is

Observation

This question was reported to have been attempted by majority of the candidates and their performance was described as satisfactory. However, most of them were reported not to calculate LABC correctly hence got wrong answers even though they were able to apply the cosine rule correctly to their wrong values. Others were not able to determine the required bearing correctly. The expected responses were as follows:

LASC = 100°. Therefore /AC/ = 82 + 132 - 2 (8)(13)cos100 which gave / AC/ = 16.4 km.

sin (LCAS) = sin100. Hence, sin (LCAB) = 13Sin100

  13                  16.4                                            16.4

Simplifying gave LCAB = 51.32°. Bearing of C from A = 180 - (50 + 51.32) = 079°.

If the distance of C east of B = BD, then BO = BC cas 40° = 13 x cas 40° = 9.96 km.

Question 10

(a) Copy and complete the table of values for the relation V = -X² + X + 2 for -3 ≤ x ≥ 3.

(b) Using scales of 2 cm to 1 unit on the x-axis and 2 cm to 2 units on the v-axis, draw a graph of the relation

y = -X² + X + 2.

(c) From the graph, find the:

(i)Minimum value of y;

(ii)Roots of the equation X² - x -2 = 0;

(iii)Gradient of the curve at x = -0.5.

Observation

This question was reported to have been attempted by majority of the candidates who were able to complete the table of values and plotted the graph correctly. However, majority ofthe candidates were reported not to draw the tangent to the curve as required. Hence they were unable to determine the gradient of the curve at

x = -0.5.

Question 11

In the diagram, L.PTQ = L.PSR = 900, /PQ/ = 10 ern, /PS/ = 14.4 cm and /TQ/ = 6 cm.

Calculate the area of quadrilateral QRST.

(b) Two opposite sides of a square are each decreased by 10% while the other two are each increased by 15% to form a rectangle. Find the ratio of the area of the rectangle to that of the square.

Observation

This question was reported not to be very popular and candidates' performance was described as not satisfactory. Majority of the candidates were reported not to apply the concept of similar triangles correctly. Others did not recognize the quadrilateral as a trapezium and so failed to use the correct formula when finding its area. Part (b) of the question was reported not to have been done satisfactorily either. Candidates were expected to show that:

/PT/ = ..../102 - 62 = 8 cm. m: =!J2L i.e ~ = 14.4.Hence, /SR/ = 10.8 cm.

                                                                                /TO/ /SR/                6 /SR/

Area of quadrilateral QRST = Yz (6 + 10.8) x 6.4 = 53.76 cm2. Some candidates were reported to have subtracted the area of triangle PQT from triangle PRS. This was also in order. In part (b) if the side of the square was y, then new breadth = 90 x y = 0.9y.

 100

New length = 115 x Y = 1.15y. New area = 1.15y x 0.9y = 1.035/.

                        100

Hence, ratio = 1.035y² : y² = 1.035 : 1 or 207:200 .

Question 12

The frequency distribution of the weight of 100 participants in a high jump competition is as

shown below:

Weight (kg)

20-29

30 - 39

40 - 49

SO - 59

60 - 69

70-79

Number of

participants

10

18

22

25

16

9

(a) Construct the cumulative frequency table.

  (b) Draw the cumulative frequency curve.

(c)   From the curve, estimate the:

(i)   median;

(ii) semi-interquartile range;

(iii) probability that a participant chosen at random weighs at least 60 kg.

Observation

This question was reported to be attempted by majority of the candidates. According to the report, candidates' performance in this question was fair. Majority of them were reported not to have read from their Ogives correctly. Others did not draw the Ogive using class boundaries.

The median was 49.5 while the first quartile(Ql) was 37.8 and the third Quartile (~)59.5.

Hence, the semi-interquartile range Q1-Q1 = 59.5 - 32.8 = 10.85 ± 1.

                                                                                          2                     2

Number of participants who weighed at least 60kg = 25. Therefore probability of choosing a

participant who weighed at least 60kg = 25= -.1 .

                                                                       100     4

Question 13

(a)The third term of a Geometric Progression (G.P) is 24 and its seventh term is 4(20/27) .Find Its irst term.

(b)Given that y varies directly as x and inversely as the square of z. If y = 4, when x = 3 and z = 1, find y when x = 3 and z = 2.

Observation

This question was reported to have been attempted by majority of the candidates and their performance was commended. However in part (a), a few of them divided the indices instead of subtracting them. A few others were not able to manipulate the fraction involved. Part (b) was also well attempted and majority of them obtained full marks.